Research on dynamics and FNTSM control of spacecraft with a film capture pocket system

Written by Copernical Team Wednesday, 28 February 2024 19:23

font size decrease font size increase font size
Print
Email

Write a comment

Scientists proposed a research on dynamics and FNTSM control of spacecraft with a film capture pocket system — Structure of the film capture pocket system. Credit: *Space: Science & Technology*

In recent years, with the significant increase in space launch activities, the number of deorbited spacecraft has sharply risen, posing a serious impact on both active orbiting spacecraft and future space activities. Traditional rope net capture systems, serving as a technology for actively deorbiting spacecraft, hold vast potential in mitigating and clearing space debris.

However, rope systems face challenges such as difficulty in maintaining shape over extended periods, susceptibility to self-entanglement, energy losses, and a reduction in the effective capture area. In contrast, thin films can fold and unfold along regular shapes, offering greater flexibility and reliability compared to tethers. They emerge as an effective solution to the entanglement issue and present a promising method for space debris mitigation and removal.

In a review article recently published in Space: Science & Technology, Professor Wei Cheng's team at Harbin Institute of Technology, in collaboration with researchers from Beijing Institute of Control Engineering and Benha University, has designed a thin film capture pocket system.

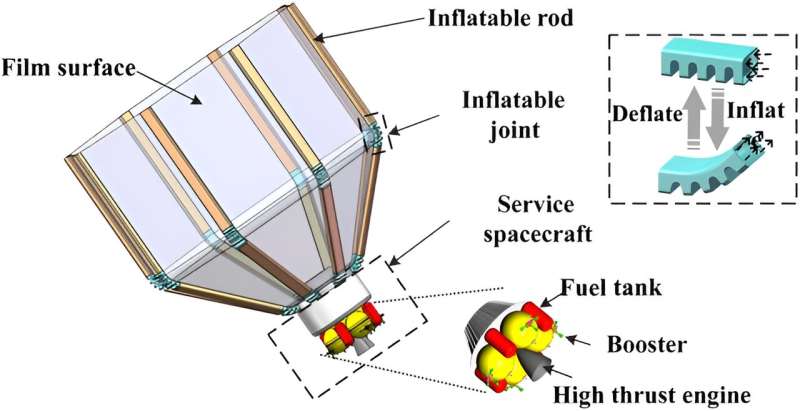
However, the flexible structure of this system is prone to significant deformation and vibrations during motion, resulting in considerable interference with spacecraft operations. To quantitatively analyze these disturbances, this study focuses on the dynamic modeling and attitude control of the thin film pocket capture system.

The research involves the development of a fast nonsingular terminal sliding mode controller (FNTSM) and a fixed time dilation observer (FxESO) integrated into an attitude-tracking control law. The effectiveness of the controller is validated through the establishment of a virtual prototype. This research provides theoretical support for the future in-orbit application of the system.

Firstly, establish the model of the capture pocket system. Utilizing a large flexible membrane structure supported by inflatable rods, the upper part forms an octagonal prism, providing a large envelope for the capture mechanism, while the lower part takes on a cylindrical shape.

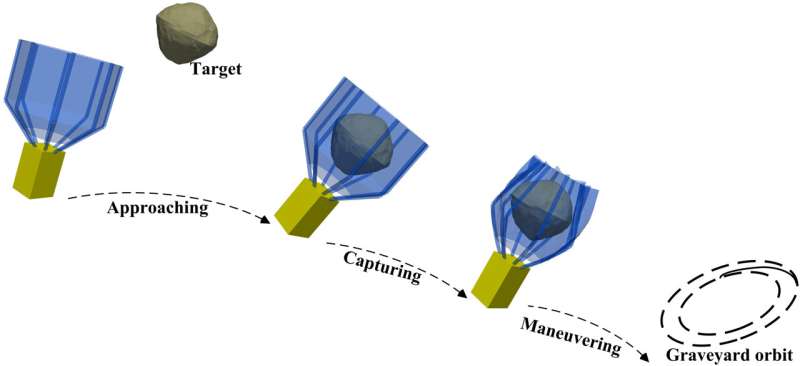
The system's deployment and retraction are achieved through the adjustment of inflation and deflation using inflatable flexible joints. The working process of the system is mainly in 3 stages. First, the spacecraft system is driven by the high thrust engine to approach the captured target. Then, inflatable flexible joints are inflated to envelop the target. Finally, the service spacecraft actively maneuvers to drag the captured target into the graveyard orbit.

Next, use the Absolute Nodal Coordinate Formulation (ANCF) to establish the dynamic model of the thin film pocket capture system. Employ high-order ANCF elements with 8 nodes to describe the motion of the film surface, representing the global position vector through interpolation polynomials Φ_i (x_i, y_i).

Describe the strain of material points using the Green–Lagrange strain tensor and substitute it into the global position vector gradient tensor Jⁱ to derive the element's motion equations. Employ the principle of virtual work to deduce the element's kinematic equations. Furthermore, introduce the controller u, angular velocity ω(ω), and unit quaternion q.

Derive the derivatives of the attitude tracking errors, including angular velocity error ω_e and attitude rotation matrix A_qe. Finally, incorporating the effects of the spacecraft's moment of inertia J_R and external disturbance d, derive the spacecraft's attitude dynamic equations.

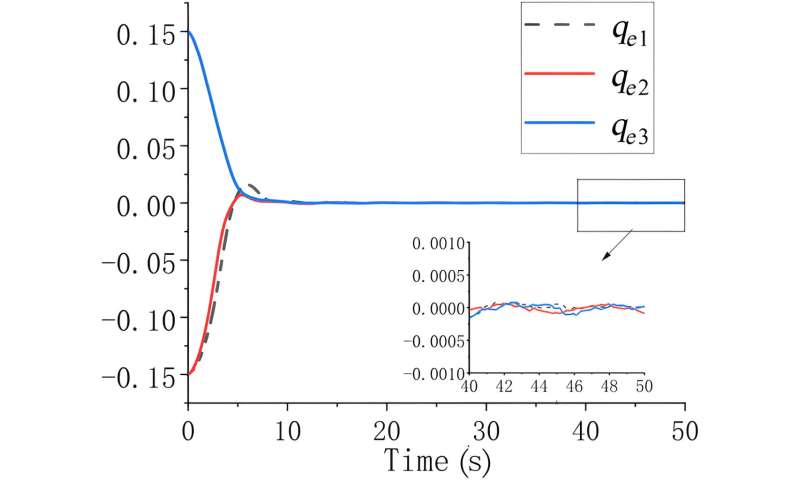
Attitude error q_e curves. Credit: Space: Science & Technology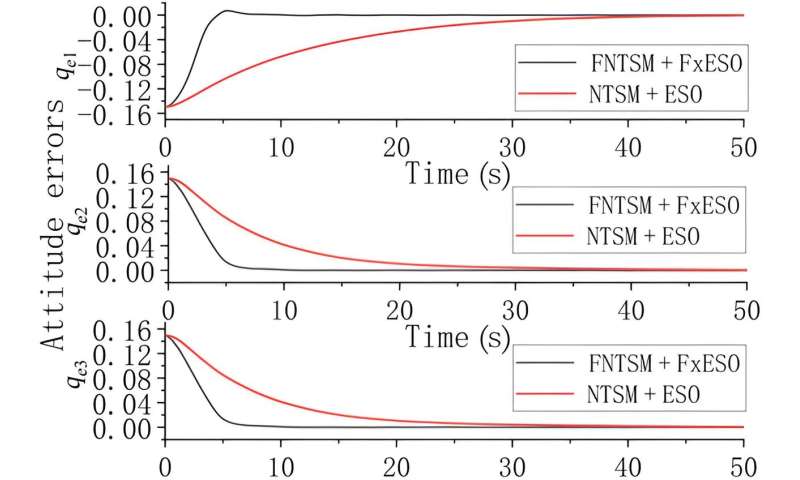
Comparison between the FNSMC + FxESO and NTSM + ESO. Credit: Space: Science & Technology

Subsequently, the author, building upon nonlinear sliding mode control, has devised a Fast Terminal Sliding Mode (FTSM) surface F. To prevent singularity issues in FTSM, a Fast Nonsingular Terminal Sliding Mode (FNTSM) surface F is designed when |q_ei| < ψ.

The introduction of a Fixed-Time Extended State Observer (FxESO) involves designing the dynamic equations for observation error, enabling estimation of uncertainties. Finally, based on FTNSM and FxESO, a spacecraft controller is designed to achieve convergence and stability within a finite time.

Following that, the author established a virtual prototype and conducted numerical simulation analyses of the relevant dynamics and control theories. The study revealed that, after spacecraft attitude maneuvers, the system gradually stabilized.

However, there were still vibrations in the flexible rods, preventing the membrane from being fully tightened, resulting in continuous wrinkles on the membrane surface. Additionally, the FNTSM + FxESO controller was compared with the Nonsingular Terminal Sliding Mode (NTSM) + Expansion Observer (ESO) controller, and the attitude errors under this controller were analyzed.

The results indicate that the FNTSM + FxESO controller brings the spacecraft to the desired attitude after 10 seconds, which is approximately 25 seconds faster compared to the NTSM + ESO controller. This significantly improves the convergence speed of the system's attitude error.

Furthermore, this controller can effectively suppress high-amplitude vibrations, keeping the steady-state attitude error at the magnitude of 10^-4. This demonstrates the high efficiency, precision, and stability performance of the proposed controller.

More information: Zhuoran Huang et al, Dynamics and FNTSM Control of Spacecraft with a Film Capture Pocket System, Space: Science & Technology (2023). DOI: 10.34133/space.0079

Provided by Beijing Institute of Technology Press Co., Ltd

Citation: Research on dynamics and FNTSM control of spacecraft with a film capture pocket system (2024, February 28) retrieved 29 February 2024 from https://phys.org/news/2024-02-dynamics-fntsm-spacecraft-capture-pocket.html

This document is subject to copyright. Apart from any fair dealing for the purpose of private study or research, no part may be reproduced without the written permission. The content is provided for information purposes only.