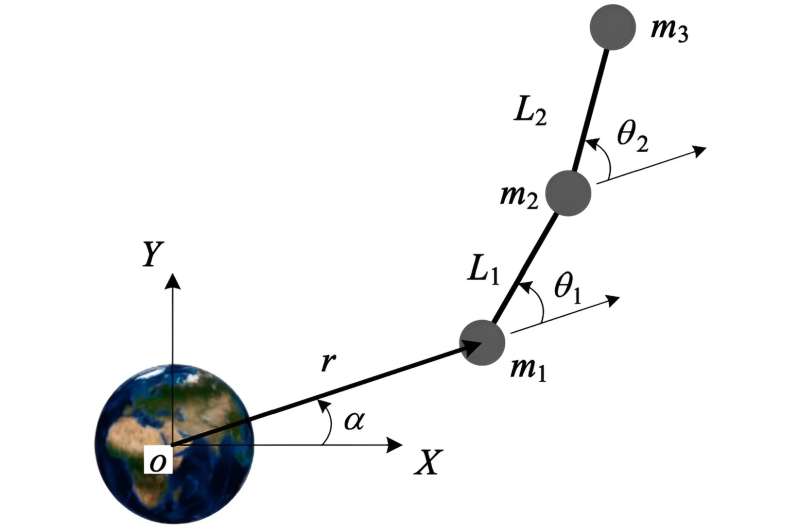
First, authors establish the motion model of a 3-body chain-type TSS in a low-eccentric elliptical orbit. Two assumptions are made: (a) the tethers are massless; (b) only the planar motion is considered. The proposed model consists of 3 point masses (m₁, m₂, and m₃) and 2 massless tethers (L₁ and L₂).

The orbit of m₁ is defined by its orbital geocentric distance r and true anomaly α; the position of m₂ relative to m₁ is determined by tether L₁ and in-plane libration angle θ₁; the position of m₃ relative to m₂ is determined by L₂ and θ₂.

The dynamic model of 3-body TSS is derived using Lagrangian formulation, and the motion equations are expressed in the Euler–Lagrange form as M(q)q̈ + C(q,q̇)q̇ + G(q) = Q with generalized coordinates q = (r, α, θ₁, θ₂, L₁, L₂)^T.

Since the TSS model in is a typical underactuated systems, the generalized coordinates are decomposed into two parts, i.e., the actuated configuration vectors (q_a = (L₁, L₂)^T) and the unactuated configuration vectors (q_ua = (r, α, θ₁, θ₂)^T).

Then, authors introduce a novel deployment scheme for the 3-body chain-type TSS. Sequential deployment strategy, ejecting satellites one by one, is employed to avoid collisions; this method utilizes the deployment techniques for a 2-body system directly; Poincaré's recurrence theorem, Poisson stability, and the Lie algebra rank condition (LARC) are used to analyze the controllability of underactuated TSS system.

A combination of exponential and uniform deployment law yields a simple and efficient deployment scheme, providing the requisite reference trajectory for satellite deployment. During the deployment process, positive tension must be guaranteed due to the characteristic tether, and to avoid tether rupture, tension must not exceed the given boundaries.

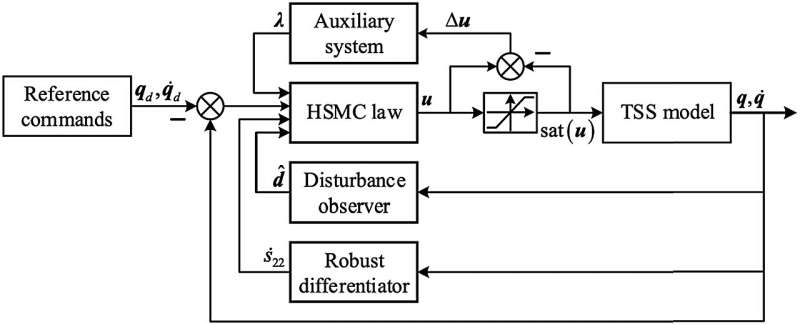
The deployment process can be simplified to a underactuated control with constrained control inputs. To address this limitation, a hierarchical sliding mode controller (HSMC) has been designed for accurate trajectory tracking. In the controller, an auxiliary system is introduced to mitigate the input saturation caused by tether tension constraint. A 3-layer sliding surface for the whole TSS is constructed. A disturbance observer (DO) is introduced to estimate second derivative signal q̈.

The uncertainty of the sliding surface and its time derivative for orbit motion (r,α) are estimated by a sliding mode-based robust differentiator.

Finally, authors present the numerical simulation and draw their conclusion. To verify the effectiveness of the proposed deployment scheme (marked as Scheme 3), two alternative deployment schemes are used for comparison. In Scheme 1, the system is regarded as 2 independent 2-body, in which the tether length L₂ remains constant, and only tension T₁ is adjustable. In Scheme 2, the system is regarded as two 2-body, but the coupling between adjacent tethers is neglected.

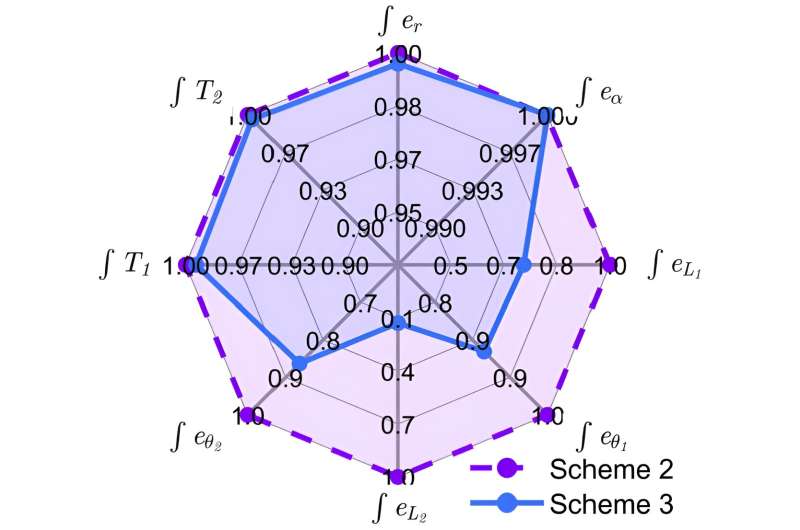
That is to say, tether L₁ only affects angle θ₁ and L₂ only affects θ₂. In Schemes 1 and 2, the deployment controller in the literature is adopted. The results show that the tether deployment error and libration angle converge to zero asymptotically in 3 h (a little more than one orbital period) under Scheme 3, and the deployment error under Schemes 1 and 2 is significantly larger than that under the proposed Scheme 3.

A comparison is made between Schemes 2 and 3 based on the integration of tracking error and tether tension. Compared to Scheme 2, the proposed HSMC explicitly takes the 3-body TSS couple into account, resulting in faster and more accurate tether deployment with a smaller in-plane angle, which further shows that a considerably improved deployment process is achieved under the proposed scheme, and confirms the effectiveness of the proposed deployment scheme.

Read more from original source...